Опубликовано пользователем Amalthea

Дворик Архимеда
Дорогой друг!
Рады приветствовать тебя на детской развивающей площадке «Дворик Архимеда» в Игуменском парке.
Здесь ты сможешь познакомиться с изобретениями Архимеда, познать с их помощью законы физики, пробежаться по беговой дорожке или поиграть в песочнице.
Пространство «Дворик Архимеда» включает шесть малых архитектурных форм (Винт Архимеда, Солнечные часы, Компас, Рычаг, Подвесной мостик, Вращающийся круг) и три игровых объекта (песочница, качели-балансир, беговая дорожка).
Для твоего комфорта следуй указаниям на табличках и перемещайся от объекта к объекту слева направо.
Реконструкция дворика выполнена в 2023 году в рамках программы «Родные города» «Газпром нефти» силами волонтерского движения «Газпромнефть-Востока» и Физического факультета Томского государственного университета.
Историческая справка
В III в. до н.э. царь Македонии Александр, покорив всю Грецию, овладев государствами Малой Азии, Персидской империей, Египтом, и частично Индией, создал огромную империю. После его смерти она просуществовала недолго и была разделена между его военно-начальниками – Диадохами – на три государства, воевавших между собой.
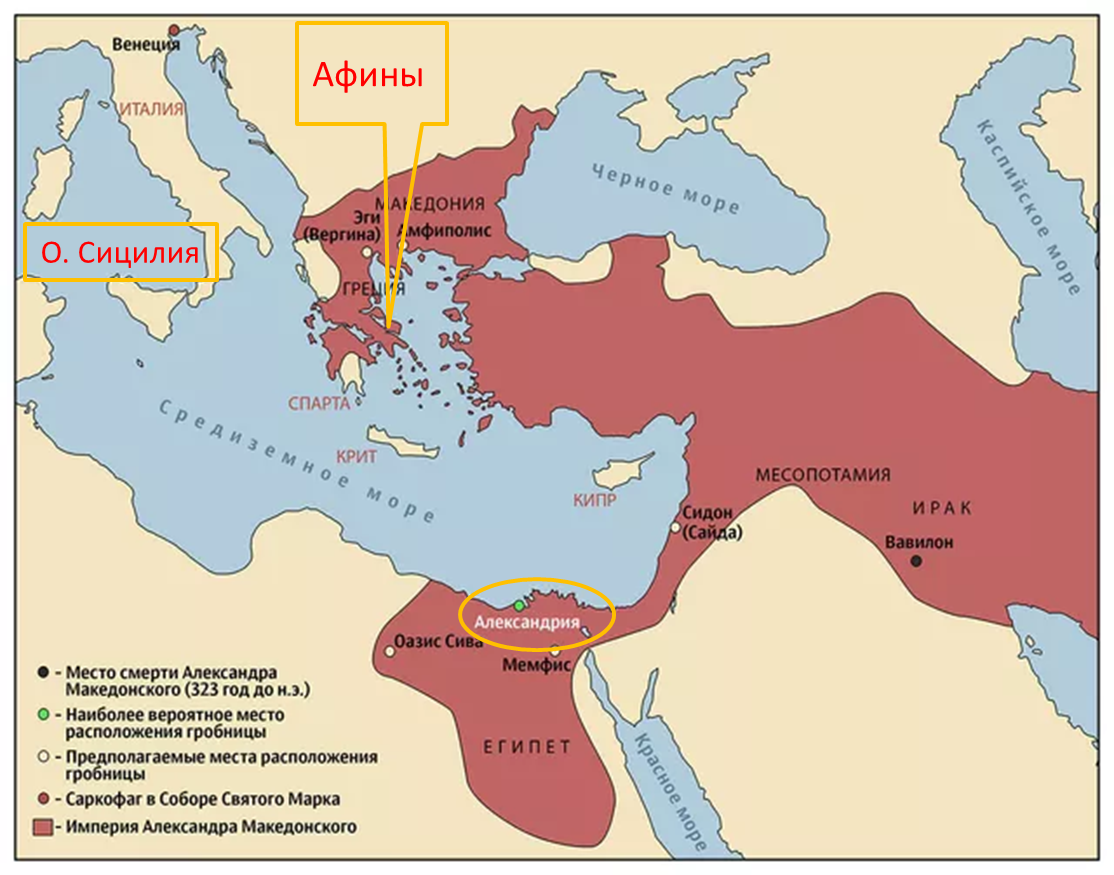
Важнейшими научными центрами были города Афины в Древней Греции и Александрия Египетская, основанным А. Македонским на завоеванной территории. Причем, если Афины были ведущими в области философии и изящной литературы. То в области астрономии, математики, филологии и медицины ведущая роль принадлежала Александрии и Александрийскому музею, где имелись обсерватории, коллекции и библиотека, имевшая, по преданию, к 48 г. до н.э. около 700000 рукописей. Египетские цари приглашали виднейших ученых из других стран и создавали им условия для научной деятельности.
Если Академия Платона и «Ликей» Аристотеля были предшественниками университетов, в которых сочетается научная и педагогическая деятельность, то Александрийский музей можно считать предшественником современных научно-исследовательских институтов.
В Александрии получили дальнейшее развитие астрономия и математика (особенно геометрия), которые выделились в самостоятельные науки. В этот же период начинает развиваться и первая область физических наук - статика жидких и твердых тел.

Архимед родился в 287 г. до н.э. в г. Сиракузы, на острове Сицилия, в семье известного астронома и математика Фидия. Образование Архимед получил в Александрии, где и начал свою научную деятельность.
Основные работы Архимеда в физике относятся к области статики и гидростатики и изложены им в ряде работ, из которых до нас дошли: "О равновесии плоских тел" и "О плавающих телах".

Вторая работа знаменита открытым Архимедом законом гидростатики. Это открытие связано с легендой, которая изложена в сочинении римского архитектора Витрувия "Об архитектуре". Гиерон II - царь Сиракуз - обратился к Архимеду с просьбой проверить, из чистого ли золота выполнена заказанная им корона, не заменили ли мастера часть золота другим металлом.
Вот как представляет себе это событие Валентин Азерников. "Случилось оно, как говорят, в бане. Бани в то время представляли собой место не только для мытья, но и для светских встреч, развлечений, спортивных игр. Поначалу Архимед, наверное, поупражнялся гирями, потом зашел в парильню, потом он поговорил с друзьями, может быть, рассказал им о последнем посещении царя Гиерона - прием у царя всегда событие, - не исключено, что поведал о его задаче и посетовал на трудность решения. А потом он, как и полагается, намылился золой и полез в ванну. И вот тут то и случилось главное. Собственно, ничего нового и не случилось, произошло то, что бывает всякий раз, когда любой человек, даже не ученый, садится в любую, даже не мраморную ванну - вода в ней поднимается. Но то, на что обычно Архимед не обращал внимания, вдруг заинтересовало его. Он привстал - уровень воды опустился, он снова сел - вода поднялась; причем поднималась она по мере погружения тела. И в этот миг Архимеда осенило. Он усмотрел в десятке раз проведенном опыте намек на то, как объем тела связан с его весом. И понял, что задача Гиерона разрешима. И так обрадовался своей случайной находке, что, как был - голый с остатками золы на теле - побежал домой через город, оглашая улицу криками: "Эврика! Эврика! - Нашел! Нашел!"". Погрузив корону царя Гиерона в чашу с водой, Архимед подсчитал объем вытесненной жидкости и сравнил его с объемом золотого слитка точно такого же, какой Гиерон передал мастерам. Объемы совпали.
Такова легенда. Главное состоит в том, что решение частной задачи привело в результате к открытию общего закона, который теперь носит его имя. Архимед подробно изложил условия равновесия тел, плавающих в жидкости, причем имеющих форму сферического или параболического сегмента. Основы гидростатики были заложены Архимедом и лишь в конце XVI и первой половине XVII столетия развиты Стевином, Галилеем, Паскалем и др.
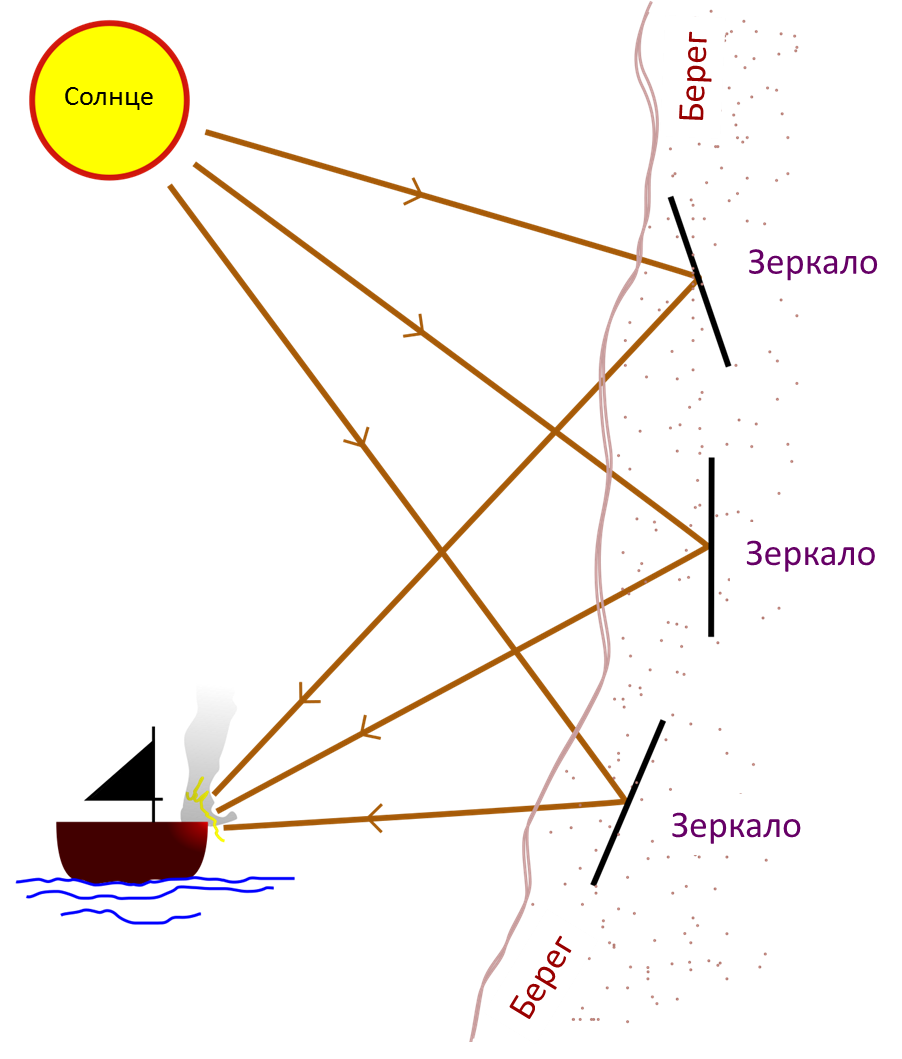
Архимеду было 23 года, когда началась первая Пуническая война между Римом и Карфагеном. Оба могущественных государства стремились склонить на свою сторону Сиракузы, но Гиерон и его приемники стремились сохранить независимость. В течение трех лет римские войска под командованием Марцелла осаждали Сиракузы. В этот период Архимед изобретал все новые машины, наводившие ужас на осаждающих. Одним из них была система зеркал, действующих вместе, как параболический отражатель солнечного света. Это устройство иногда называют Огнем Архимеда. Художественная интерпретация представлена на табличке – фрагмент фрески Джулио Парижи.
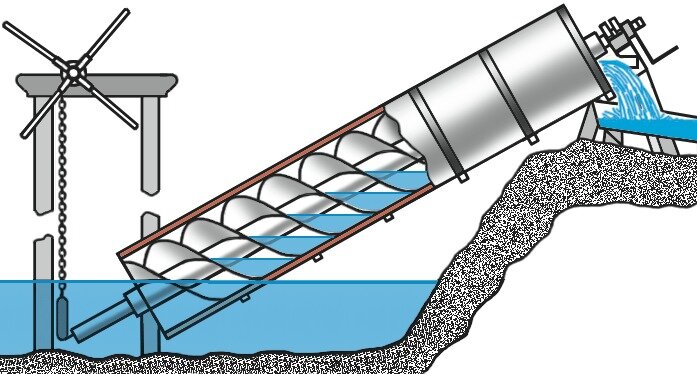
Наиболее гениальным изобретением был винт для подъема воды, который и сейчас называется Архимедовым винтом. По оценке Галилея, это изобретение "не только великолепно, но просто чудесно, поскольку мы видим, что вода поднимается в винте, беспрерывно опускаясь". Винт использовался как для подъема воды на возвышенности (до 4 м), так и для осушения низменностей и для откачки излишней воды с кораблей. Изобретение Архимеда используется и в настоящее время в нефтедобыче, агропромышленности и угольной промышленности.
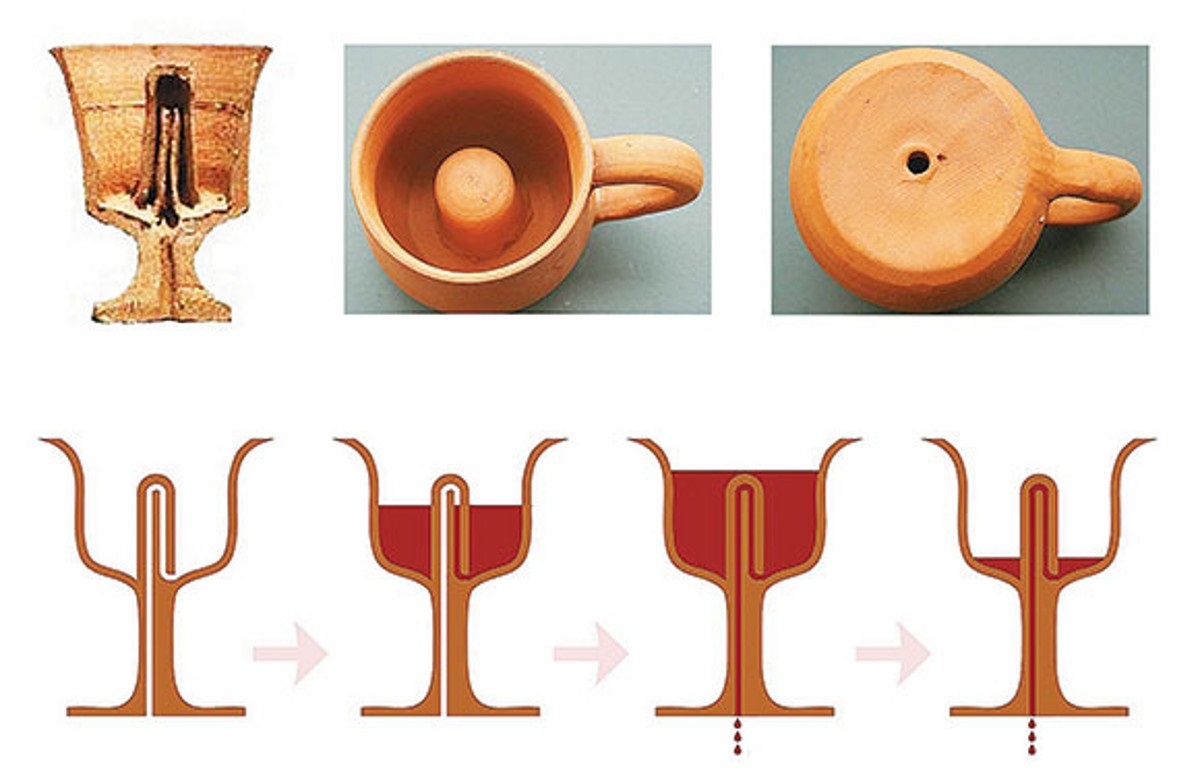
Верхняя чаша сконструирована как чаша Пифагора (V в. до н.э.). Жители родного города Самос (Греция) испытывали постоянную нехватку пресной воды. Сосуд был изготовлен для ее экономии. Устройство работает по принципу сообщающихся сосудов — пока уровень жидкости находится ниже отметки на внутренних стенках, кружкой можно пользоваться по назначению. Как только чаша переполняется, содержимое попадает в изогнутую трубку и вытекает наружу.
Также чашу Пифагора называют Кружкой жадности.
В порту г. Сиракузы Архимед построил немало блочно-рычажных механизмов для подъема грузов. Известна его фраза: "Дайте мне точку опоры, и я вам подыму весь мир". Эту фразу он сказал своему родственнику Гиерону - царю Сиракуз. И на практике показал царю, как можно двигать и поднимать большие тяжести. Плутарх так описывает это событие: "Архимед приказал посадить на царскую грузовую триеру, с громадным трудом с помощью многих рук вытащенную на берег, большой экипаж, положить на нее обыкновенный груз, и, усевшись на некотором расстоянии, без всяких усилий, спокойно двигая рукой конец блока, стал тянуть к себе триеру так тихо и ровно, как будто она плыла по морю. Пораженный этим, царь оценил важность механики и упросил Архимеда построить для него машины, которые служили бы как для защиты, так и для нападения в какой угодно осаде". Архимед стал первым ученым, разработавшим конструкции катапульты. Рычаг дает выигрыш в силе. Можно прикладывать меньшую силу на большем плече, расстоянию от точки опоры.
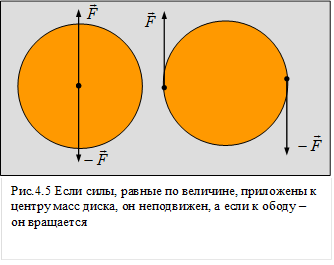
Вращающийся круг тоже демонстрирует принцип рычага. Только силы приложены в противоположных направлениях. Правило Рычага лежало в основе строительной и военной техники, он позволял поднимать большие тяжести, преодолевать значительные сопротивления. Отсюда и пошло название механика. Греческое слово "механе" означало орудие, приспособление, осадную или театральную машину, ухищрение. В течение многих веков механика рассматривалась как наука о простых статических машинах.
Вращательное движение представляет одно из наиболее общих и поразительных свойств Вселенной. Планеты и их спутники, звезды, вращающиеся вокруг своих осей, планеты, вращающиеся вокруг Солнца, вращающиеся двойные звезды, звезды и их спутники, вращающиеся вокруг центров своих галактик, многие галактики входят в состав вращающихся вихревых скоплений. В более простых случаях это смерчи, водовороты, вращение колес экипажей, вращение игрушечного волчка, вращение электронов в атомной модели Бора и т.д.



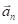 и тангенциальное ускорение
и тангенциальное ускорение 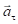 . Соответственно, уравнение движения можно спроецировать на направления этих ускорений
. Соответственно, уравнение движения можно спроецировать на направления этих ускорений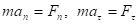 ,
,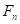 – проекция силы, действующей на материальную точку, на направление, перпендикулярное к скорости, а
– проекция силы, действующей на материальную точку, на направление, перпендикулярное к скорости, а 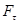 – проекция силы на направление скорости. Тангенциальное ускорение
– проекция силы на направление скорости. Тангенциальное ускорение 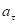 можно выразить через угловое ускорение бетта.
можно выразить через угловое ускорение бетта.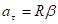 ,
,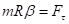 . (4.1)
. (4.1)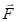 , действующей на точку и направлением на центр окружности через альфа. Из рис. 4.4 видно, что
, действующей на точку и направлением на центр окружности через альфа. Из рис. 4.4 видно, что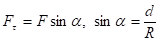 ,
,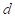 – длина перпендикуляра, опущенного из центра окружности на линию действия силы, называемая плечом силы.
– длина перпендикуляра, опущенного из центра окружности на линию действия силы, называемая плечом силы.С учетом этих соотношений получим, что
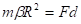 .
.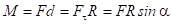 называется моментом силы относительно оси вращения. Уравнение движения (4.1) принимает вид
называется моментом силы относительно оси вращения. Уравнение движения (4.1) принимает вид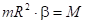 . (4.2)
. (4.2)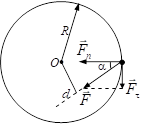
Необходимо учесть, что сила имеет направление и может как увеличивать угловую скорость, так и уменьшать. Условно можно принять, что одно из направлений движения точки, например против часовой стрелки, является положительным. Тогда момент силы можно считать положительным, если сила увеличивает скорость вращения в направлении против часовой стрелки, и отрицательным - в противоположном случае.
Полученное уравнение движения (4.2) сходно с уравнением Ньютона
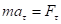 : вместо силы в нем фигурирует ее момент относительно оси вращения, вместо ускорения
: вместо силы в нем фигурирует ее момент относительно оси вращения, вместо ускорения 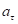 – угловое ускорение бетта, место массы заняла комбинация
– угловое ускорение бетта, место массы заняла комбинация 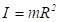 , зависящая не только от массы, но и от ее расположения относительно оси вращения. Эта комбинация называется моментом инерции материальной точки относительно оси вращения. Момент инерции при вращательном движении играет ту же роль, что и масса при поступательном движении точки по прямой. Чем больше момент инерции, тем больший требуется момент силы, чтобы изменить угловую скорость. Значение момента инерции, как видим, определяется не только массой, радиальное положение массы даже более существенно, так как
, зависящая не только от массы, но и от ее расположения относительно оси вращения. Эта комбинация называется моментом инерции материальной точки относительно оси вращения. Момент инерции при вращательном движении играет ту же роль, что и масса при поступательном движении точки по прямой. Чем больше момент инерции, тем больший требуется момент силы, чтобы изменить угловую скорость. Значение момента инерции, как видим, определяется не только массой, радиальное положение массы даже более существенно, так как 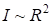 . Например, раскрутить камень, привязанный на длинной веревке, труднее, чем в случае короткой веревки.
. Например, раскрутить камень, привязанный на длинной веревке, труднее, чем в случае короткой веревки.С учетом момента инерции уравнение (4.2) примет вид
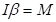 . (4.3)
. (4.3)Аналогию с уравнением поступательного движения можно продолжить, если его записать в виде
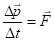 , где
, где 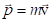 – импульс точки. Так как угловое ускорение
– импульс точки. Так как угловое ускорение 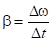 , а момент инерции материальной точки при движении по окружности не зависит от времени, уравнение вращательного движения материальной точки (4.3) можно записать в виде
, а момент инерции материальной точки при движении по окружности не зависит от времени, уравнение вращательного движения материальной точки (4.3) можно записать в виде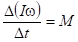 . (4.4)
. (4.4)Учитывая, что
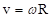 , можно записать
, можно записать 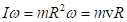 . Выражение
. Выражение 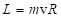 называется моментом импульса материальной точки относительно оси вращения. Таким образом, уравнение вращательного движения относительно неподвижной оси принимает вид
называется моментом импульса материальной точки относительно оси вращения. Таким образом, уравнение вращательного движения относительно неподвижной оси принимает вид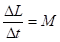 . (4.5)
. (4.5)Хотя второй закон Ньютона для вращательного движения рассмотрен на примере материальной точки, тот же вид имеет уравнение вращательного движения абсолютно твердого тела вокруг неподвижной оси.
Абсолютно твердым телом можно считать тело, размеры и форму которого можно считать неизменными. Понятие абсолютно твердого тела является идеализацией реальных тел, так как все тела под действием приложенных сил в той или иной степени деформируются, то есть меняют форму и размеры. Однако, если деформации малы, то ими можно пренебречь и рассматривать тело как абсолютно твердое. Такое тело можно разбить на отдельные достаточно малые элементы, которые можно было бы рассматривать как материальные точки. При вращении тела вокруг неподвижной оси все эти точки движутся с одинаковыми угловыми скоростями по окружностям, центры которых лежат на оси вращения. Для каждого элемента массой Dm можно записать уравнение вращательного движения (4.5), а затем все эти уравнения почленно сложить. При этом сумма моментов внутренних сил будет равна нулю, так как согласно третьему закону Ньютона эти силы равны по величине и направлены по одной прямой в противоположные стороны. В результате получится уравнение вида
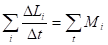 .
.После суммирования этих уравнений получится уравнение
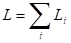 ,
,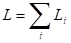 – момент импульса тела относительно неподвижной оси вращения, а
– момент импульса тела относительно неподвижной оси вращения, а 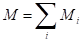 – суммарный момент всех внешних сил, действующих на тело, относительно оси вращения.
– суммарный момент всех внешних сил, действующих на тело, относительно оси вращения.Момент импульса
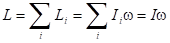 . Здесь
. Здесь 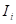 – момент инерции отдельных элементов тела
– момент инерции отдельных элементов тела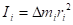 ,
,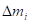 – масса отдельного элемента, а
– масса отдельного элемента, а  – расстояние от этого элемента до оси вращения. Таким образом, момент инерции тела
– расстояние от этого элемента до оси вращения. Таким образом, момент инерции тела  зависит не только от массы тела, но и от распределения массы относительно оси вращения. Для абсолютно твердого тела момент инерции – постоянная величина, поэтому уравнение движения (4.4) можно записать в виде
зависит не только от массы тела, но и от распределения массы относительно оси вращения. Для абсолютно твердого тела момент инерции – постоянная величина, поэтому уравнение движения (4.4) можно записать в виде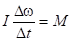 или
или 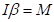 .
.Пример 1.

Пример 2.

Чтобы облегчить поворот тяжелой детали, рабочий использует рычаг, позволяющий сообщить детали требуемое угловое ускорение за счет небольшого усилия
МЕХАНИЧЕСКОЕ РАВНОВЕСИЕ
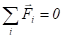 ,
,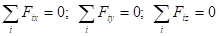 .
.Очевидно, что тело может покоиться только по отношению к одной определенной системе координат. В статике изучают условия равновесия тел именно в такой системе. Необходимое условие равновесия можно получить также, рассмотрев движение центра масс системы материальных точек. Внутренние силы не влияют на движение центра масс. Ускорение центра масс определяется векторной суммой внешних сил. Но если эта сумма равна нулю, то ускорение центра масс
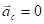 , а, следовательно, скорость центра масс
, а, следовательно, скорость центра масс 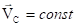 . Если в начальный момент
. Если в начальный момент 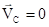 , то центр масс тела остается в покое.
, то центр масс тела остается в покое.Таким образом, первое условие равновесия тел формулируется следующим образом: скорость тела не меняется, если сумма внешних сил, приложенных в каждой точке, равна нулю. Полученное условие покоя центра масс является необходимым (но недостаточным) условием равновесия твердого тела.
Пример 3.

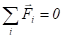 .
.Может быть так, что все силы, действующие на тело, уравновешены, тем не менее, тело будет ускоряться. Например, если приложить две равных и противоположно направленных силы (их называют парой сил) к центру масс колеса, то колесо будет покоиться, если его начальная скорость была равна нулю. Если же эти силы приложить к разным точкам, то колесо начнет вращаться. Это объясняется тем, что тело находится в равновесии, когда сумма всех сил равна нулю в каждой точке тела. Но если сумма внешних сил равна нулю, а сумма всех сил, приложенных к каждому элементу тела, не равна нулю, то тело не будет находиться в равновесии, возможно, как в рассмотренном примере, вращательное движение. Таким образом, если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.
Чтобы получить второе условие равновесия, воспользуемся уравнением вращательного движения
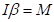 , где
, где 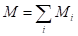 – сумма моментов внешних сил относительно оси вращения. Когда
– сумма моментов внешних сил относительно оси вращения. Когда 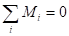 , то и бетта = 0, а значит угловая скорость тела не меняется . Если в начальный момент w = 0, то тело и в дальнейшем не будет вращаться. Следовательно, вторым условием механического равновесия является требование равенства нулю алгебраической суммы моментов всех внешних сил
, то и бетта = 0, а значит угловая скорость тела не меняется . Если в начальный момент w = 0, то тело и в дальнейшем не будет вращаться. Следовательно, вторым условием механического равновесия является требование равенства нулю алгебраической суммы моментов всех внешних сил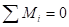 .
.В общем случае произвольного числа внешних сил условия равновесия можно представить в следующем виде
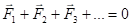 ,
,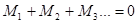 .
.
Пример 4.

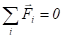 ,
, 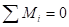 .
.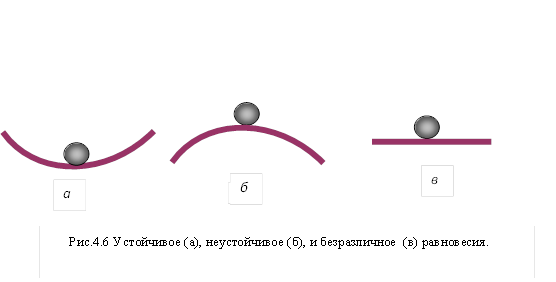
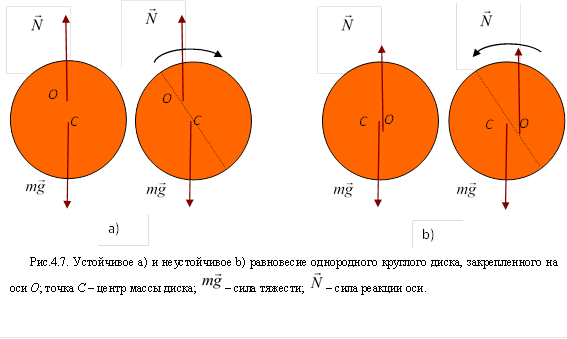
Для тела, имеющего неподвижную ось вращения, возможны все три вида равновесия. Безразличное равновесие возникает, когда ось вращения проходит через центр масс. При устойчивом и неустойчивом равновесии центр масс находится на вертикальной прямой, проходящей через ось вращения. При этом, если центр масс находится ниже оси вращения, состояние равновесия оказывается устойчивым (рис.4.7а). Если же центр масс расположен выше оси – состояние равновесия неустойчиво (рис.4.7б)
Особым случаем равновесия является равновесие тела на опоре. В этом случае упругая сила опоры приложена не к одной точке, а распределена по основанию тела. Тело находится в равновесии, если вертикальная линия, проведенная через центр масс тела, проходит через площадь опоры, то есть внутри контура, образованного линиями, соединяющими точки опоры. Если же эта линия не пересекает площадь опоры, то тело опрокидывается.
Пример 5.

Интересным примером равновесия тела на опоре является падающая башня в итальянском городе Пиза, которую по преданию использовал Галилей при изучении законов свободного падения тел. Башня имеет форму цилиндра высотой 55 м и радиусом 7 м. Вершина башни отклонена от вертикали на 4,5 м.
Пиза́нская ба́шня получила известность благодаря тому, что она сильно наклонена. Башня «падает». Высота башни составляет 55,86 метров от земли на самой низкой стороне и 56,70 метров на самой высокой стороне. Её вес оценивается в 14700 тонн. Текущий наклон составляет около 5,5°. Вертикальная линия, проведенная через центр масс башни, пересекает основание приблизительно в 2,3 м от его центра. Таким образом, башня находится в состоянии равновесия. Равновесие нарушится и башня упадет, когда отклонение ее вершины от вертикали достигнет 14 м. По-видимому, это произойдет очень нескоро.
Полагали, что кривизна башни задумана зодчими изначально – ради демонстрации своего незаурядного умения. Но куда более вероятно другое: архитекторы знали, что строят на крайне ненадежном фундаменте, и потому заложили в конструкцию возможность легкого отклонения.
Когда возникла реальная угроза обрушения башни, за нее взялись современные инженеры. Ее затянули в стальной корсет из 18 тросов, фундамент утяжелили свинцовыми блоками и параллельно укрепили грунт, закачивая под землю бетон. С помощью всех этих мер удалось уменьшить угол наклона падающей башни на полградуса. Специалисты говорят, что теперь она сможет простоять еще как минимум 300 лет. С точки зрения физики принятые меры означают, что условия равновесия башни стали более надежными.
Источник: Анохина И.Н., Нявро В.Ф. МЕХАНИКА // Методические рекомендации для преподавателей // Томск, 2007 г.

